백준

[1912번] 연속합

1912번: 연속합 첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다. www.acmicpc.net 풀이 n = int(input()) list = list(map(int, input().split())) dp = [0] * n # 최대 연속합 dp[0] = list[0] for i in range(1, n): dp[i] = max(list[i], dp[i-1]+list[i]) # list[i] / 이전최대연속합 + list[i] # print(dp) print(max(dp))

[10844번] 쉬운 계단 수(2차원 DP)

10844번: 쉬운 계단 수 첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다. www.acmicpc.net 분석 D[N][H] : 길이가 N인 계단에서 H높이로 종료되는 계단 수를 만들 수 있는 경우의 수 D[i][0] : 0인 경우, 뒤에 1만 올 수 있음 ➔ D[i][1] D[i][j] : 1~8인 경우, -1, +1 높이 올 수 있음 ➔ dp[i][j]= dp[i-1][j-1] + dp[i-1][j+1] D[i][9] : 9인 경우, 뒤에 8만 올 수 있음 ➔ D[i][8] 풀이 import sys input=sys.stdin.readline # 길이 n=int(input()) # dp[계단길이][계단높이] dp=[[0 for j in range(11)] for i in ran..

[11726번] 2×n 타일링

11726번: 2×n 타일링 2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다. www.acmicpc.net 분석 D[N] : 길이 N으로 만들 수 있는 타일의 경우의 수 D[N-1] : n-1까지 타일이 채워져있는 경우 ➔ 새로운 타일 1개를 채워 N길이를 만듦 D[N-2] : n-2까지 타일이 채워져있는 경우 ➔가로로 타일 2개를 래워 N길이를 만듦 D[N] = D[N-1]+D[N-2] 풀이 # 2*n크기 직사각형을 2*1/1*n으로 채우는 방법의 수 n = int(input()) d=[0]*1001 # n의 최댓값 1000 d[1]=1 d[2]=2 for i in range(3, n+1..

[14501번] 퇴사

14501번: 퇴사 첫째 줄에 백준이가 얻을 수 있는 최대 이익을 출력한다. www.acmicpc.net bottom up n = int(input()) s = [list(map(int, input().split())) for i in range(n)] dp = [0 for _ in range(n+1)] for i in range(n): for j in range(i+s[i][0], n+1): if dp[j] < dp[i] + s[i][1]: dp[j] = dp[i] + s[i][1] print(dp[-1]) top down n = int(input()) dp = [0]*(n+2) # 오늘부터 퇴사일까지 벌수있는 최대수입 (점화식 테이블) t=[0]*(n+1) # 상담에 필요한 일수 p=[0]*(n+1)..

[24042번] 횡단보도(다익스트라)

24042번: 횡단보도 당신은 집으로 가는 도중 복잡한 교차로를 만났다! 이 교차로에는 사람이 지나갈 수 있는 $N$ 개의 지역이 있고 그 지역 사이를 잇는 몇 개의 횡단보도가 있다. 모든 지역은 횡단보도를 통해 직, www.acmicpc.net 분석 시간 역행 불가, 이미 지난 가중치로 지나갈 수 없음 ➔ 주기 이전 소요 시간 ≤ 지금 이용하는 시간 값이 될 때까지 M을 여러 번 더하여(곱하여) 사용 풀이 import heapq import sys input = sys.stdin.readline n, m = map(int, input().split()) graph = [[] for _ in range(n+1)] for i in range(m): a, b = map(int, input().split())..

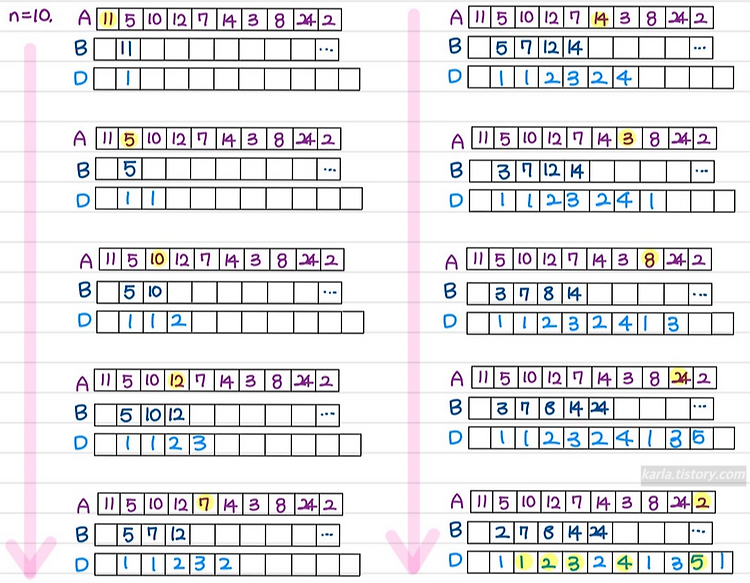
[14003번] 가장 긴 증가하는 부분 수열5 (LIS, 이분탐색)

14003번: 가장 긴 증가하는 부분 수열 5 첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000) www.acmicpc.net 분석 D[i] : 0~i까지 i를 포함하는 가장 길게 가하는 수열의 길이 A[i]를 i번째 수열의 값이라고 정의하면 D[k]는 A[i]>A[K]를 만족하는 최대 수열의 길이 즉, A[i]보다 작은 값을 지니고 있는 수열의 최장 증가 수열의 길이들 중 최댓값을 찾아 해당 값에 +1 한 값을 D[i]에 저장 D[i] = max({D[k]}) +1 (k=1~i-1) D 리스트를 맨 뒤에서부터 탐색해 최댓값과 동일 값을 가지는 최초 inde..